Graph of the week: learning about learning
[latexpage]
An important concept in understanding production efficiency of complex items is the notion of a learning curve. The term has passed into common usage, with ‘steep learning curve’ being synonymous with ‘really hard to master’ (in all sorts of contexts). That badly misrepresents its actual technical meaning; a steep learning curve actually means that something is easy to master. In the case of the production of things like warships, it means that the workforce concerned is getting on top of technical difficulties quickly.
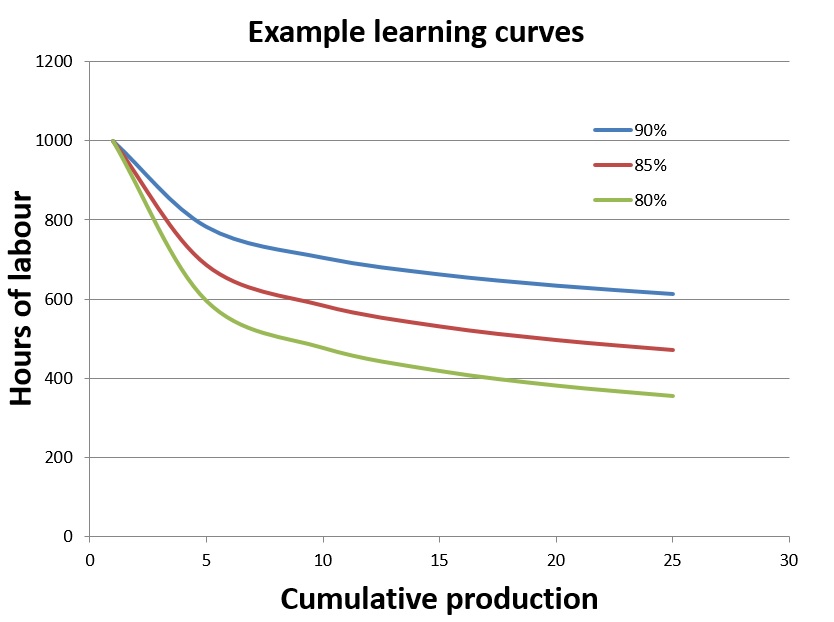
A learning curve can be drawn in a number of complementary ways, but for the purposes of analysing defence projects, the most useful form plots the number of person-hours required to produce each item as production rolls along. Here’s an illustrative example. If the first item takes 1,000 labour-hours to produce, and the learning (in its technical meaning) is 90%, then every time the production numbers double the labour required for each item reduces by 10%. I.e. the second one takes 900 hours, the fourth takes 810 hours, the eighth 729 hours etc. By the time the 25th is produced, it’s taking a little over 600 hours. (See the blue curve in Figure 1, click graph to enlarge) As production times come down, unit labour costs fall as well, though the more productive workforce often shares some of the gains in the form of higher wages.
Now look at the other two curves, labelled 85% and 80%. These are the result of steeper learning curves, and they show the labour hours (and thus costs) coming down more quickly as production continues.
Those numbers weren’t chosen at random. It turns out that numbers around the 80–90% figure are typical for industrial applications. In the defence sector, shipbuilding has a steeper learning curve than aerospace production. The simple reason is that building ships is much more hands-on than building modern aircraft—people do a lot more of the actual producing of the finished item than machines. People benefit more from practice than machines do.
In fact, we can break down the production of an aircraft or ship into several sub-stages, each of which has its own learning factor. For example, in aircraft production (PDF, slide 11), the largely automated fabrication stage has a learning around 90%, while the more human-intensive assembly phase is closer to 75%. The overall learning curve will depend on the relative time taken in each of those stages.
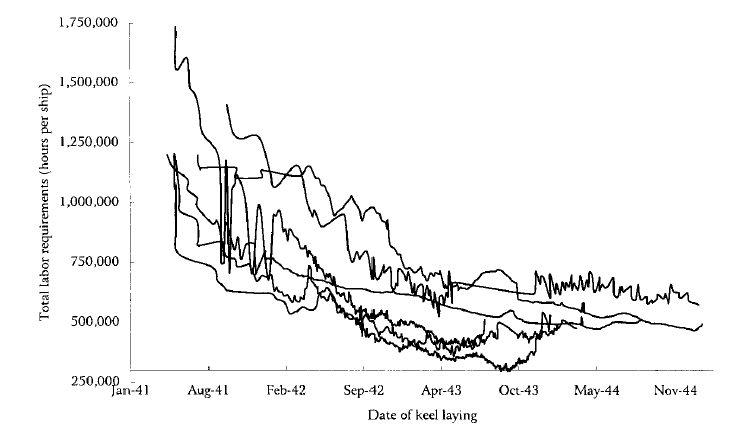
To show this isn’t just theory, let me finish with a real world example, but with a warning that real life doesn’t produce nice smooth curves like the examples above. Any changes in design or materials used, for example, will tend to kick the curve upward again, until the new design and techniques are mastered.
Here’s a graph (click to enlarge) from a study of the production of ‘liberty ships’ in American shipyards in WWII (PDF). The various yards showed different levels of learning, but all of them managed to reduce the number of labour-hours per ship from 1.2 million or more to less than half the starting point. In this case, making efficient use of a limited labour force and producing ships quickly to replace those being lost at ferocious rates in the Battle of the Atlantic were both strategic necessities. The contracts put in place with shipbuilders provided incentives to do both.
As a final comment, learning curves show why it’s often desirable to avoid producing items like ships in small numbers: you get all of the disadvantages of the early unpractised workforce, but not the long-term advantages of the mature learning curve. Building ten Anzac frigates was almost guaranteed to give a better overall result in terms of production efficiency than a run of three AWDs. Eight future frigates, on the other hand, would again allow for the benefits of learning to help amortise the early costs (not to mention one-off costs associated with design, engineering and infrastructure) across a larger fleet.
Andrew Davies is senior analyst for defence capability and director of research at ASPI.
Note for the mathematically inclined:
For 90% learning, the ‘learning parameter’ λ = 0.9. It’s related to a power law for the number of hours $T(n)$ for the nth production item relative to the first: if $T(n)=T(1)n^{mu}$, then $lambda=2^{mu}$, or $mu = frac{lnlambda}{ln2}$. For $lambda$ = 0.9, $mu$ = -0.152.